放射性崩壊のシミュレーション

崩壊定数が0.005で放射性崩壊のシミュレーションを行なった。以下にその結果を記す。

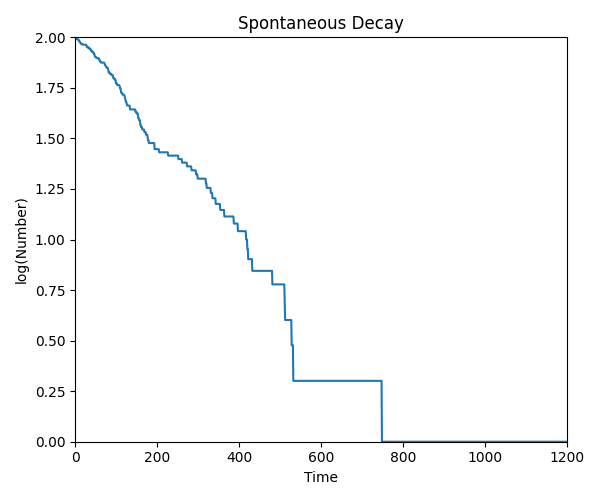
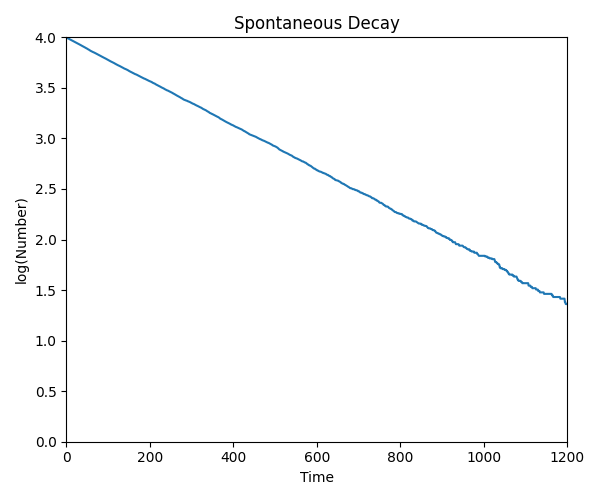
上の三つのグラフは、経過時間開始後に傾きが一定の部分があるように見える。つまり、log(N(t))∝-a*tと表せる(ここでaは正の定数)。対数と指数の関係より、N(t)=exp(-a*t)となり、放射能の時間依存性が導ける。
このグラフでは表現できないが、プログラム実行時は、Pythonのwinsoundモジュールを使って、粒子数が減る度にビープ音が鳴るように設定し、さながらガイガー・カウンターのようだった。
粒子数が大きい場合は、開始後にしばらく上の時間依存性に従うが、粒子数が小さい場合は傾きが直線の部分は見出しにくい。
今回は乱数を用いて粒子数は減少するようにプログラムをPythonで組んだ。粒子数が少ない場合に、崩壊の様子をどう記述できるのかという興味に駆られたし、崩壊定数とN=0になるまでの時間との関係も知りたい。

あとがき
定数aの決定は、傾きを見ればよいが、グリッドを付ければよかったと今さらながらに後悔する。