コンピュータで「微分」する

例えばtの関数f(t)があって、それをtで微分したいときに、解析学を学んでいたらすぐに答えは出るだろう。f(t)の関数形が分かっていたら、である(しかし関数形が分かっていなかったらどうだろう？)。分かっていても、微分はコンピュータで近似的に求めるのが良いように思える。まずは、下の図を見て欲しい。

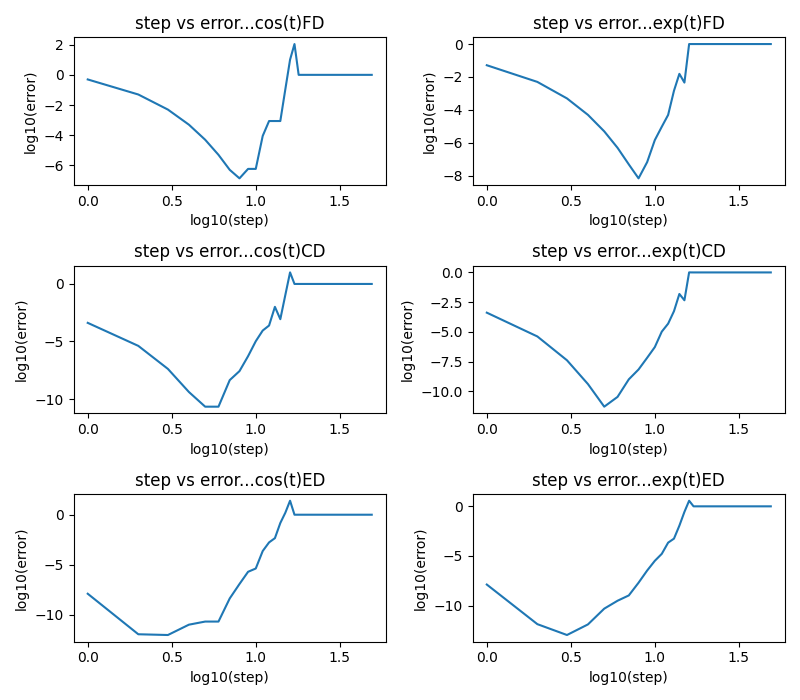
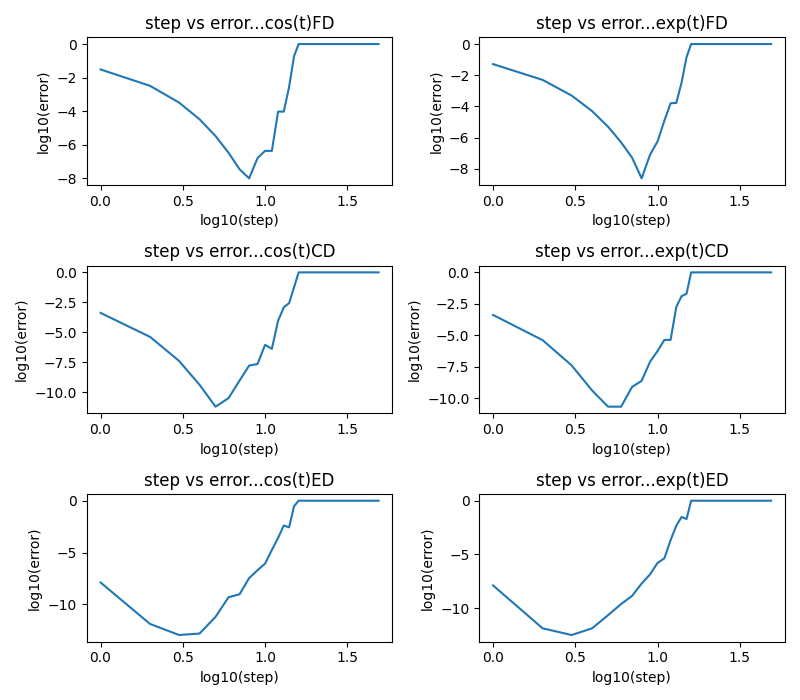
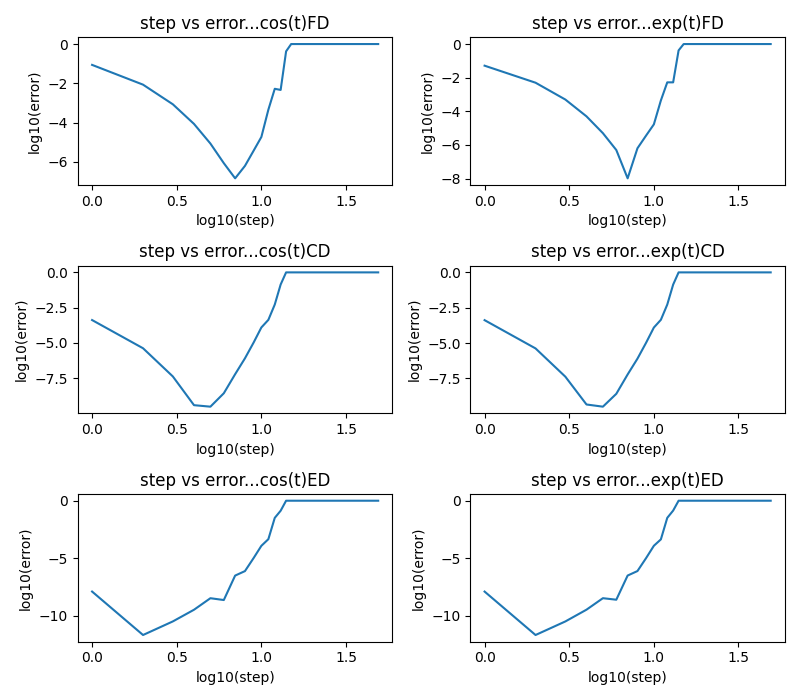
相対誤差は、ステップ数が多いほど小さいわけではない。それぞれのグラフに極小値が見られる。どのグラフも、極小値を迎えると急激に相対誤差が大きくなっているのも見られる。更に、差分の精度が上がってゆく(FD→CD→ED)と、相対誤差が極小となるステップ数が小さくなっているのも見てとれる。ここで、FD、CD、EDをどのように計算したかというと、以下に示す通り：

FD=(f(t+h)-f(t)/h
CD=(f(t+h/2)-f(t-h/2))/h
ED=((8*f(t+h/4)-f(t-h/4))-(f(t+h/2)-f(t-h/2)))/(3*h)

もちろん、hは小さくとる。例えばf(t)=cos(t)をtについて微分したら-sin(t)になるのは分かっている。しかしコンピュータは極限の操作は行えないから、差分で求めるしかないのだ。

極限とはなんだろう？
私は高校三年で極限を学んだが、「無限大にする」ということはある意味想像の話ではないだろうか(語弊があるかもしれないが)。最近、微分を考える時にそう思えてならない。もちろん私は解析学の結果に茶々をいれるわけではない。しかし、「具体的な」数値を入れないと近似的な値をはじき出さないコンピュータを見ていると、数学とは何だろうと不思議な気持ちになる。「近似」、「厳密な結果」…。

極限とは何だろう？
数学とは何だろう？