ラグランジュ補間の練習

数式を追ってばかりでは、物理をやっている気がしないのは本当のことか。時には実験も行わなくては。
今回はラグランジュ補間の練習をした。ラグランジュ補間、というのは実験データを曲線で近似する補完法のひとつである。ラグランジュ補間のアルゴリズムに従ってプログラムを組めたことは大いに有益であった。Scipyのライブラリにラグランジュ補間を一瞬で行なうのがあるらしい(私はだいぶ後からになってそれを知った)が、いまはプログラミングの練習をしているので、自力でプログラムを組むことに専念した。その結果、得られたのが次のグラフである。

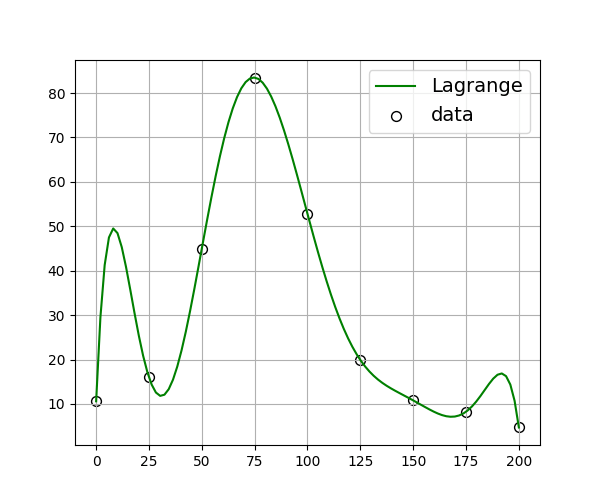
キャプションにも書いてあるが、ラグランジュ補間では実験値の始めと最後付近で妙なピークが見られる。これはラグランジュ補間公式が高次の多項式を用いることによる。9個のデータがあったら、8次多項式ができる。その8次多項式をもとにして上図では緑のプロットができている。

今回の練習では、グラフを描く(Matplotlib)、代数方程式を表す(Sympy)、数値の取り扱い(Numpy)、あとは自力でラグランジュ補間を実装(二つのfor文とif文をうまく使う)した。これらの練習を通して、プログラミングの能力が上がったことに間違いはないだろう。

今後の計算物理学の話も、是非付き合って欲しい。