フィッティングするということ

ここ数日は、最小二乗法をPythonで行なうことを学んでいた。まずは下の図を見てほしい。

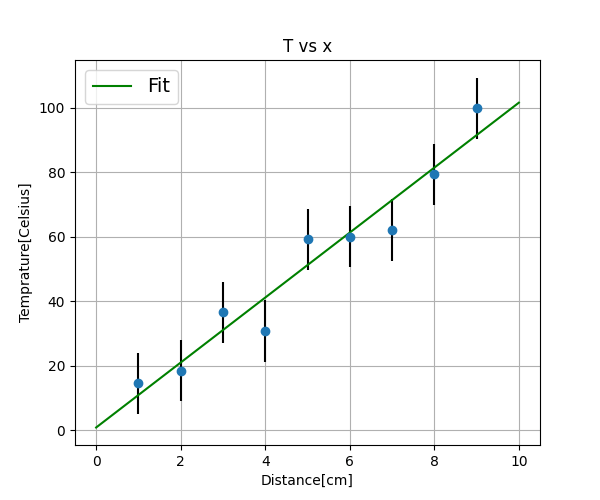
図は、温められた棒の端(Distance=0)から温度(Temparature)を計った結果得られた実験データである。青い丸がまず生のデータで、それに最小二乗法を実施し緑色の直線をひいた。

最小二乗法は、学生の時に良く学んだ。実験ではかなりお世話になるデータの解析方法である。懐かしさを感じながらテキストを読んでいた。

次に載せるのは、最小二乗法を用いてデータに曲線をフィットした例である。

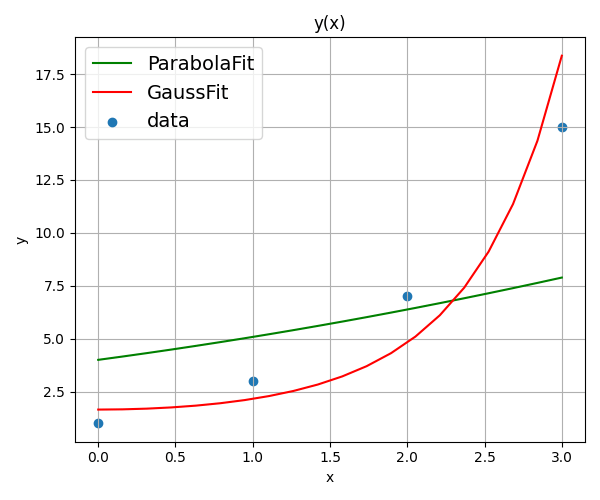
緑の線は放物線だが、そうは見えないくらい直線に近い。アルゴリズムが間違っていたのだろうか。一方、赤い曲線がガウス型関数、A*exp(-b*x^2)でフィッテングさせたものである。こちらは、どうやら綺麗にデータに沿っているように見える(見える、だけであって、実際はもっと別の関数でフィッテングできるかもしれない)。

今回は、最小二乗法をゼロからプログラミングし、データに関数をフィットさせることを行なった。なかなか骨の折れるプログラミングだったが、これをマスターすれば、実験データの解釈がより一層深く、詳しくなるだろう。

計算物理学の冒険はまだまだ続く。