フィッティングするということ２

さあ、最小二乗法のひとまずの課題を終えた。
とにかく下の図を見てほしい。

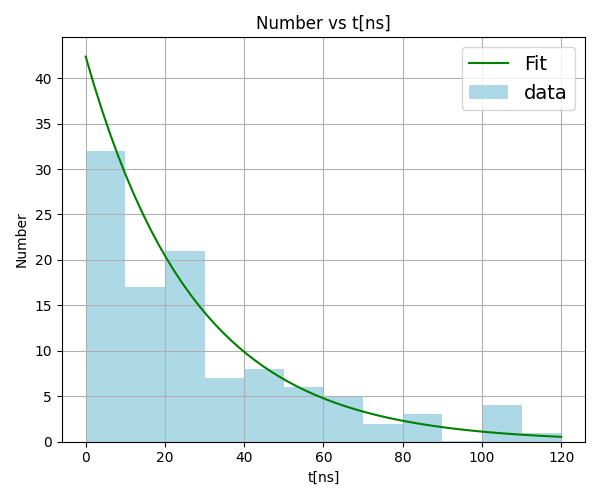
テキストの課題をこなしたいがために結果をブログにアップロードした。実験データは水色の棒グラフである。これに最小二乗法を実施して緑色の指数関数をフィットさせた。曲線をフィットさせたが、最小二乗法で直接得られるのは直線だ。上手く変数変換できれば、指数関数を描くことができる。

崩壊の微分方程式を解くと、Number(time)という関数は、Number=N0*exp(-time/tau)と書ける。式中のN0は粒子数の初期値、tauは、この場合、π中間子の「寿命」である。最小二乗法ではこのtauも得られる。びっくりだ。

さて、最小二乗法メインの課題はここまでだ。次からは、次なる課題をこなそうと思う。引き続き、計算物理の旅を続けよう。