ビリアル定理を学ぶ

宇宙物理学で、最初にその定理の存在を知った。私は物理学の学徒だったが、その定理の存在はそれまで知らなかったものだから、学徒時代の学習環境が相当悪かったのだと思ったものである。しかしまあそんな過去のことを悔やんでも仕方がない。学んでいる今とその先を見据えることが大事なのだ。過去のことを気にするのは、実験を行なった状況と最初においた仮定のことだけでよい。

さて、つまらない話はやめて話の核心を述べよう。まず、例によって例のごとく、下にある図を見てほしい。

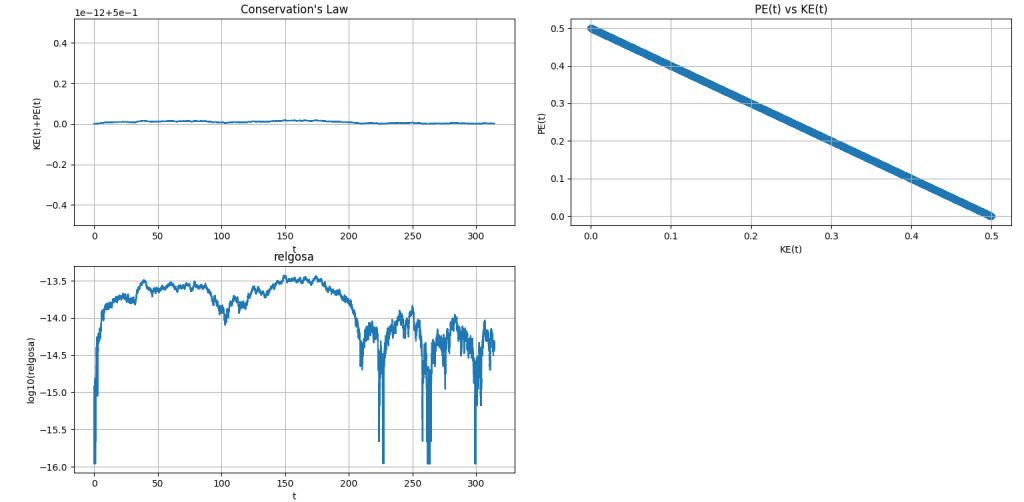
注目すべきは、右上の図である。運動エネルギーとポテンシャルエネルギーが負の相関になっていることだ。高校物理の始めで習う、「力学的エネルギー保存の法則」だ。運動エネルギーが増えたらポテンシャルエネルギー(高校物理では「位置エネルギー」)が減り、運動エネルギーが減ったらポテンシャルエネルギーが増える。総エネルギーは変化しない(このことを、「総エネルギーは保存する」という)ことを如実に表している。

その定理、「ビリアル定理」はこのエネルギー保存則に関する定理である。相変わらず勉学不足で、この定理の神髄を述べるには至らない。しかしそれを言い訳にして、この投稿をやめるわけにはいかない。科学者はべき思考の塊で、常に「～しなければならない」という思考を持っている。私も実際べき思考が強いのだ。ゆえに、記述を続けよう。

力学的エネルギー保存則を詳しく書くと、上図の記法で書くのならば、
KE+PE=const.
である。これは力学的エネルギーに限った話ではない。上図の場合は1つの質点の系だった。質点系から剛体系、剛体から連続体系へと広げることができる。剛体までであると慣性モーメントの時間変化、連続体では内部エネルギーの項が上の式に加わる。
宇宙物理学では、星の安定性を調べる際にこのビリアル定理が用いられる。

具体的な話をしよう。
系が力学平衡にあるとき、慣性モーメントの時間変化が0になるので、ビリアル定理は次のようになる。
2*KE+PE+3*(γ-1)*UE=0
ここでPEは重力エネルギー、γは比熱比、UEは系の内部エネルギーである。いろいろな平衡条件を課し、このビリアル定理を表現する。上では「力学平衡」、ほか「静水圧平衡」などがある。静水圧平衡は、星の静的な状態を調べるのに重要な平衡条件である。また、気象学の分野でも重要な平衡条件である。

以上の議論は、私のオリジナルが全くなく、やはり勉学不足が祟っているのかと思うばかりである。しかし過去のことを思ってもしょうがない。私はいまと先のことを見据えるべきなのだ(べき思考だ！)。これからも、私が勉学したものや、割と自由に自身の考えを述べる時があるので、興味があれば付き合ってほしい。

ここまで読んで下さり、感謝するばかりである。