引き続き、微分方程式を解く

計算物理学の勉学も結構進んできた。しかし私はその道を歩み始めたばかりだ。今までなしてきたことをまだ俯瞰することができない。俯瞰するには早すぎると感じていている。

さて、まず次の図を見てみよう。

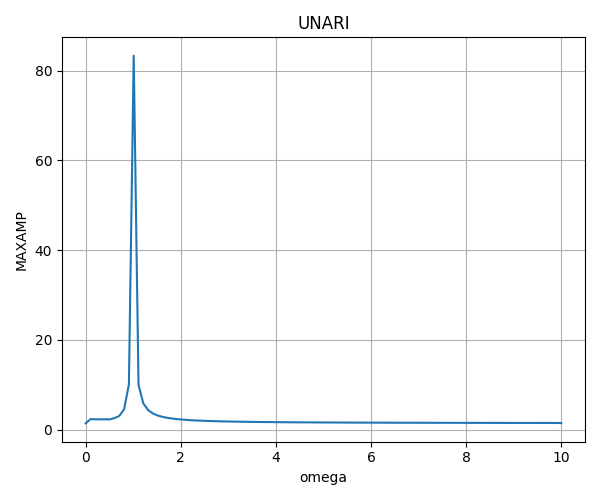
図のキャプション通りである。なお余談だが、私が組んだコードでは、このグラフを描くのに370秒もかかってしまった。余計な計算をする箇所があったのが原因と考えられる。今後は注意したいと思う。

さて、今回の投稿の本番だ。次の3つの図をまず掲載する。微分方程式を解くときに大いに参考にできる例である。

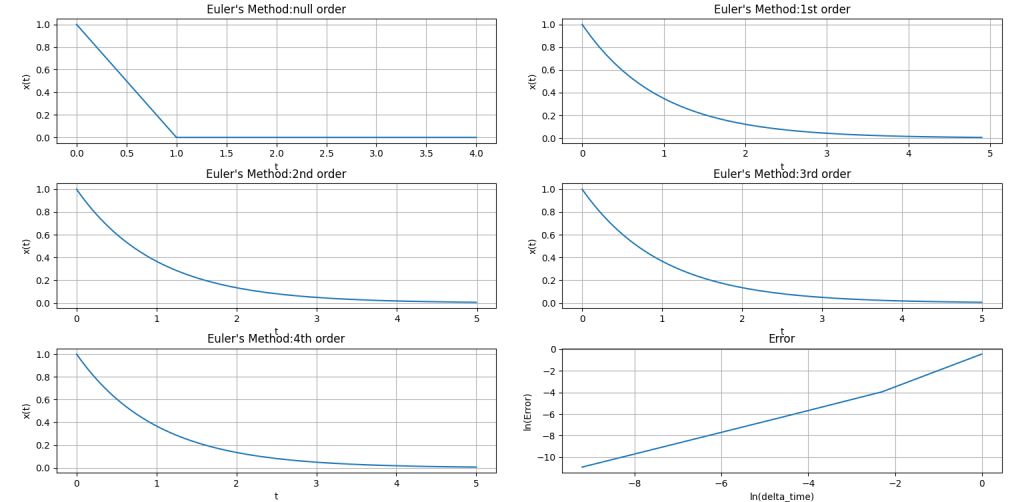
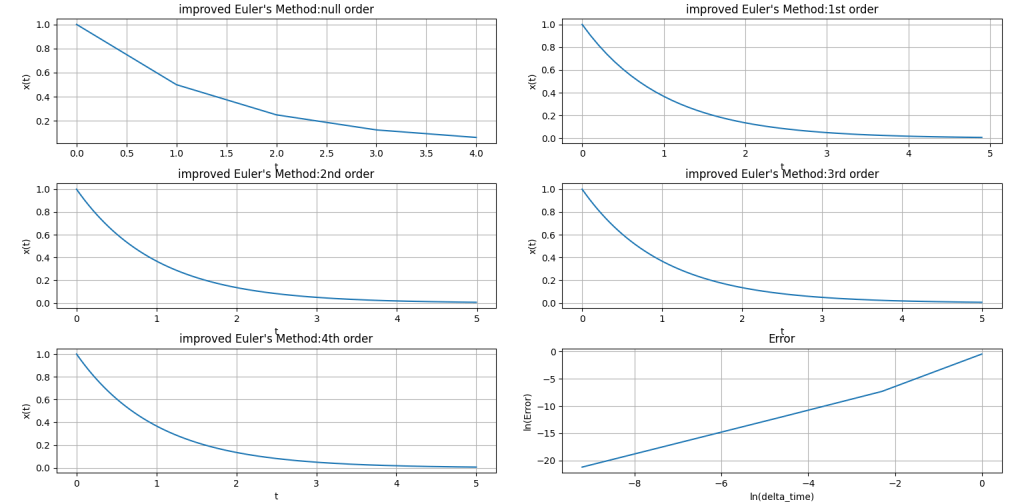
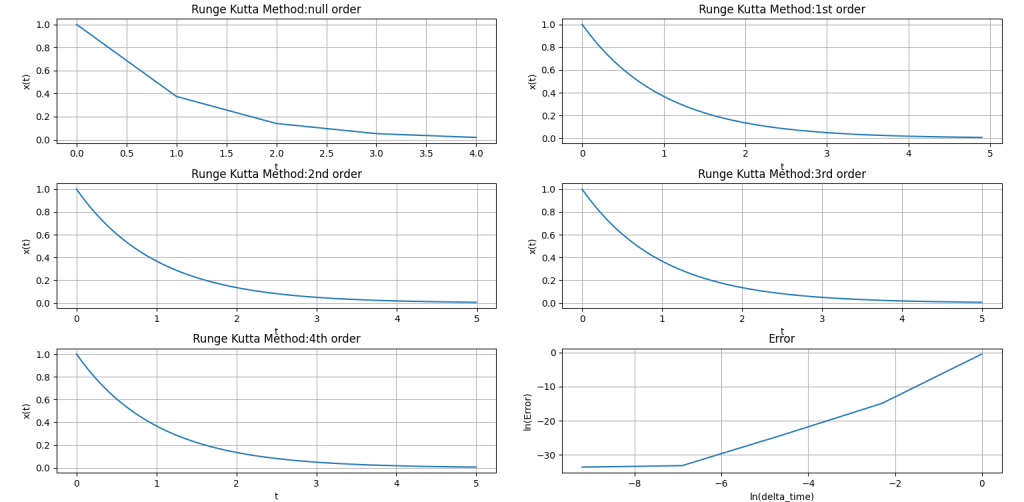
これらの図のキャプションに書いてある微分方程式(1)とは、次に示すとおりである。

—equation(1)—
dx/dt=-x
x(0)=1

これは解析的に解けるごく簡単な微分方程式だ。その解析解は、

—solve(1)—
x(t)=X0*exp(-t)

である。X0は初期条件を満たす定数。この解析解と、三つの方法を使って得られる数値解とを比べたのが右下の誤差とステップ幅のグラフというわけだ。グラフを人間の目で見る限り、ルンゲ-クッタ法以外はほぼ直線に見える。これは何を意味しているのだろうか？直線ということは、数学的には次のように書けることを意味する。

ln(Error)=α*ln(delta_time)+β

ここでα、βは定数を表す。要するに線形回帰しているわけだ(もっと易しくいうと、一次関数として書ける、という意味)。この式を変形しよう。

Error=C*delta_time^(α)

ということになる(高校数学で習った対数と指数の関係を思い出そう)。ここでCは新しい定数である。この式は、誤差はステップ幅のべき乗に比例しているということを示すものである。つまり、ステップ幅を小さくすれば、誤差も小さくなる、ということだ。なんとなく思っていたことが、コンピュータと高校数学の知識で理解できた。主たる定数α、βの具体的な値は、直線の傾きを調べることによって知ることができる。

今回は、微分方程式を三つのアルゴリズムで解き、ステップ幅と誤差の関係を明らかにした。次の計算物理学の話題は少し難しいので、復習がてらに数値積分でもしてみようかと思う。台形則、シンプソン則、ガウス求積法をもう一度コードを作ってみるのだ。また、微分方程式を解くことをもっと掘り下げて、ベクトル場を描いてみたい。それらが私の次なる課題である。

今回も話に付き合っていただけて幸いである。ありがとうございました。