なんという魂の震え！

久しぶりの計算物理学に関する投稿だ。私は少しばかり気が高まっている。
早速、次のグラフを見てほしい。

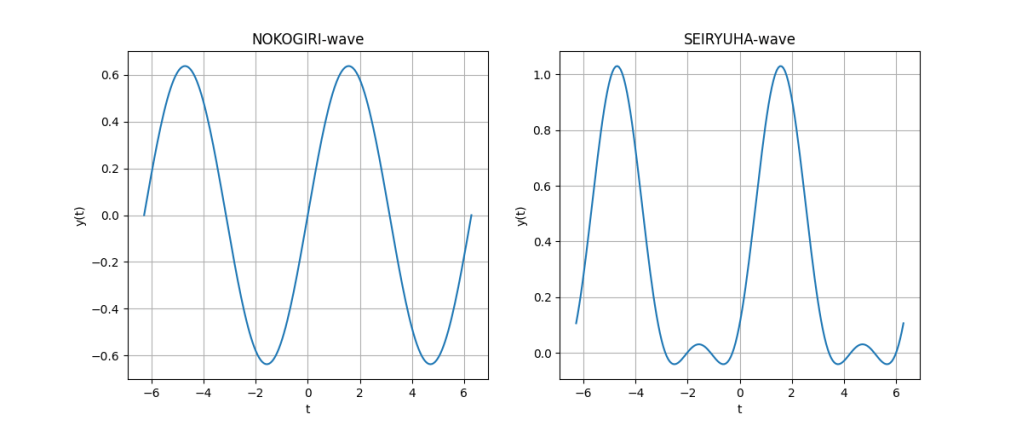
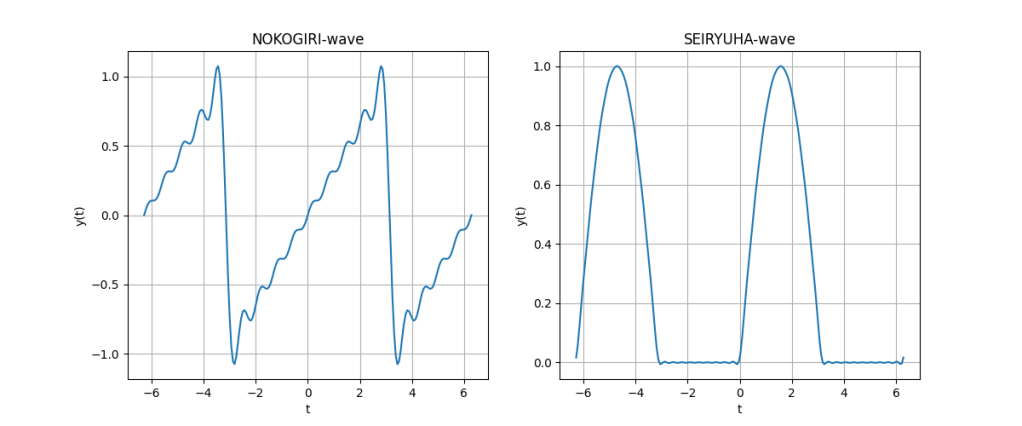
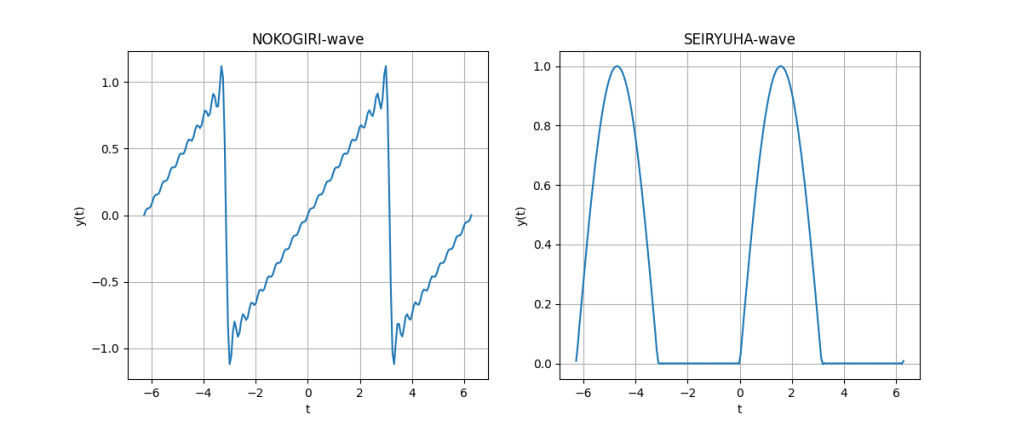
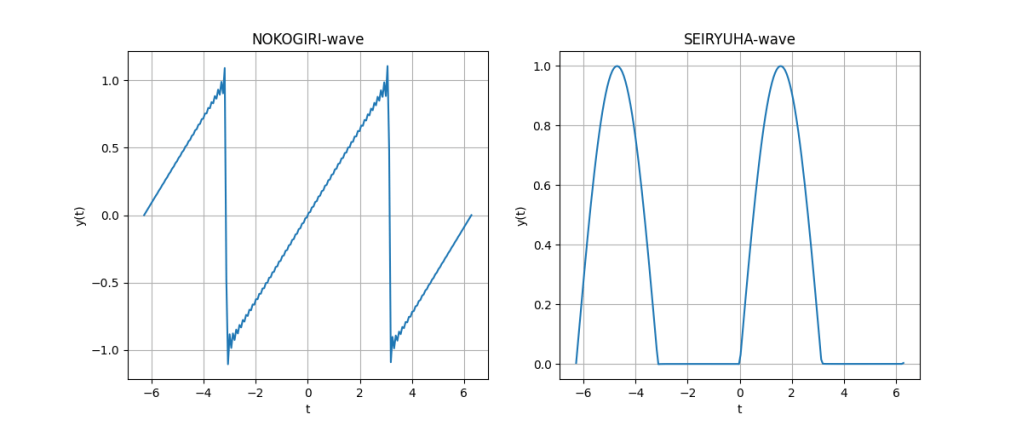
フーリエ解析の始めのほうでは、必ず学ぶことになるのこぎり波。学びたての頃は、おそらくびっくりするひとが多いのこぎり波である。なにか意図的に考えた波形が、数学的にこんな風に表せられるだなんて。私はそう思ったものだ。

計算物理も、いよいよ大詰めを迎えている。これでも、「初歩の」大詰めだ。

グラフのキャプションにあるnという整数は、フーリエ級数の部分和のことである。式が複雑になるのでここには示さない(もっとも、いまのWordPressのサービスでここにLaTeXのように数式が書ければ話は別だが)。
視覚的に理論が分かるのは、フーリエ解析の特徴であると言えるだろう。部分和の最後のインデックスを示すnを大きくすればするほど、波形は「考えた波形」に近づく。これは驚くべきことだ！

私はフーリエ解析だけではなく、フーリエ本人についても興味がある。この記事を持って、フーリエ解析の勉学の始めとしたい。訂正。「始め」ではなく「再開」だ。

たぶんこれからもいろいろな「波形」をこのブログに載せることになるだろう。色々課題はある。前の投稿で述べた数値積分など未解決の話題は沢山ある。しかし、前に進むことも大事だ。

さて、どんどん学習を続けよう。