やっと描けた「物体の軌道」

まず、見てほしいものがある。それはこれだ。

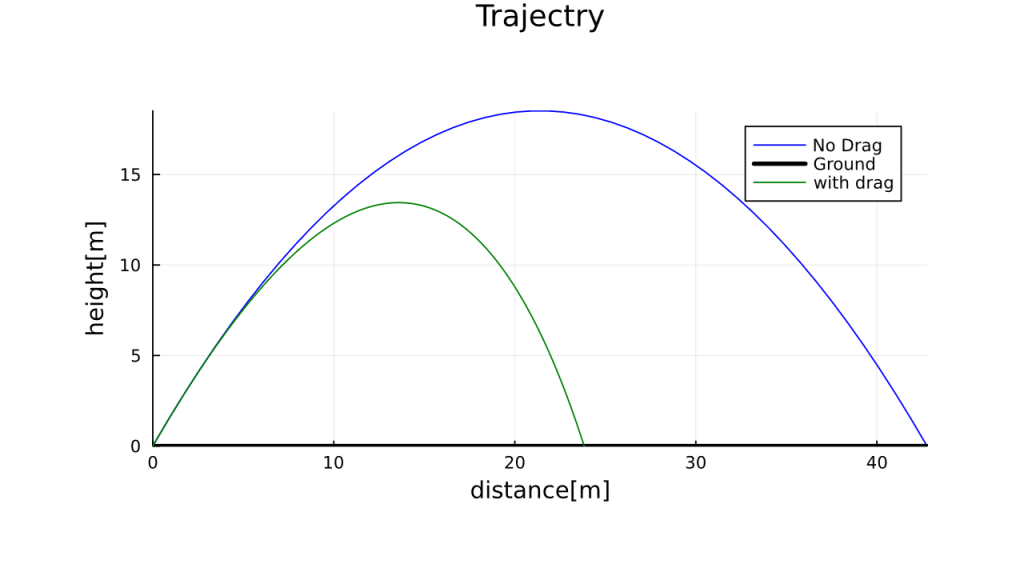
前投稿と同じ、やっと描けた放物体の軌道である。これもマスタするのに半年以上かかった。最終的にはAIにコードを教えてもらうということに。残念な話ではあるが…。

詳しい話にいこう。
物体は、次の式で表せる水平加速度ax、鉛直加速度ayで運動するとした：
ax=-k*(abs(v)^n)*vx/abs(v)
ay=-k*(abs(v)^n)*vy/abs(v)-g
ただしここでvx,vyはそれぞれ物体の水平速度、鉛直速度である。大雑把に言えば、kは空気抵抗の大きさ、nは速度によって空気抵抗がどれくらい強くなるかを表す。gはもちろん重力加速度である。

このグラフをJuliaで描いた。まず始めに加速度を定義し、4次のルンゲ-クッタ法で数値計算を行ない、vx、vy、x、yを求めていった。

微分方程式を数値的に解く方法がマスタできたからには、これからいろいろ自然現象を表すことができるようになるだろう。多くの自然現象は微分方程式で表せるからである。

次なる課題は…、ロトカ-ボルテラ・モデルを、ルンゲ-クッタ法で解く。