(2)バーンスレーのシダ

さて、いつものごとく、次の図を見てほしい。

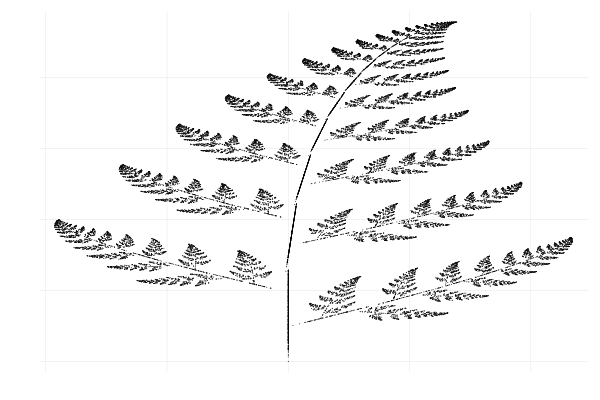
JuliaでPlotsパッケージを用い、描いた。プログラムのコードとしては40行ほど。それなのに、こんなに美しいシダが描けるなんて。私はびっくりした。コードを書いている途中は、どんな図になるのか全く想像できなかった。反復と条件分岐が得意なコンピュータのおかげである。

私は当分、このシダを観葉植物として、部屋において置く(というつもりで頭の片隅で大切にしたい)。

アフィン変換に詳しくならなければならない。アフィン、と聞くと相対論で聞く「アフィン接続」が真っ先に思い浮かぶ。アフィン変換は、拡大縮小・移動・回転の変換のようだ。まるで、複素関数について考えているようだ。

コンピュータゲームでよく出てくる、ゲーム中にキャラクタが世界を歩くシーンがある。そのなかで、実際の自然界によく似た森や草原が出てくる。そこに描かれて「再現」されているものは、なんだろう？　木はどんな風に「再現」されているのだろう。世界の再現という意味で、ゲームは色々と高度なことをやっていると思う。

シダというと、草食恐竜が古代に食べていたものという印象がある。私はシダ本来についてはそのことしか知らないのだが、数学を学ぶ上で、シダという例を知ることができて大変に嬉しい。

これからも、フラクタル探訪の旅は続く。